Search Help banner
The University of Melbourne Atomic Force Microscope Cantilevers
(Calibration method of Sader)
The University of Melbourne
Back to Introduction
Online calibration Online calibration Online calibration
iPhone1, Web App1 & Global Calibration Initiative2*

* banner
Online calibration

1. Sader Method for a set of rectangular/non-rectangular cantilevers.
2. Sader Method GCI for all cantilever types.


Background Theory

The spring constants of AFM cantilevers are often required in applications of the AFM. For force measurements where normal deflection of the cantilever is monitored, the normal spring constant, which relates the applied normal force to the normal deflection of the cantilever, is required (see Fig. 1 below for a schematic).

Normal spring constant
Fig. 1: Schematic illustration of the normal spring constant.

In Lateral Force Microscopy, the torsional spring constant, which relates the applied torque to the angle of twist of the cantilever is important (see Fig. 2 below for a schematic).
Torsional spring constant
Fig. 2: Schematic illustration of the torsional spring constant.

Here, we briefly outline the Sader method for calibrating the normal spring constant of rectangular AFM cantilevers, as well as the Torsional Sader method which enables the calibration of the torsional spring constant of rectangular AFM cantilevers. We also describe the physics underpinning the method and its extension to cantilevers of arbitrary shape.

First, though, we note that both techniques require the plan view dimensions of the rectangular cantilever (length and width), which can be obtained with sufficient accuracy using an optical microscope. Furthermore, the resonant frequency and quality factor of the peaks is also needed. These are typically obtained by measuring the thermal noise spectra of the unloaded AFM cantilever, and fitting the response of a Simple Harmonic Oscillator (SHO) with added white noise floor,

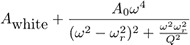
Equation of SHO

to the fundamental power spectrum resonant peak, see Fig. 3 below. A Mathematica ® notebook which performs this fit is available to download here.

Fitting a SHO to the thermal noise spectra.
Fig. 3: SHO fit to thermal noise power spectrum. The red line is the response of a SHO, whilst the black circles are experimental data from the thermal noise spectrum.

Once the required quantities are measured, the normal and torsional spring constants of the cantilever can be determined using the following techniques, provided that the following conditions are met:
  1. That the length of the cantilever greatly exceeds its width, which in turn greatly exceeds its thickness;

  2. That the quality factor is much greater than unity.

In practice, the first requirement is typically satisfied for practical rectangular cantilever, whilst the second requirement is usually satisfied when the cantilever is immersed in air.

Sader method

The normal spring constant of a rectangular AFM cantilever can be determined using the Sader method [1], which states

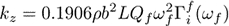
Normal spring constant using the Sader method

where L and b are the length and width of the cantilever, respectively, ρ is the density of the fluid, ωf and Qf are the (radial) resonant frequency and quality factor of the fundamental resonance peak, respectively, and Γif is the imaginary part of the hydrodynamic function given by Eq. (20) of Ref. [2].

In order to assist the reader, the Sader method has been implemented in an online calibrator, meaning that no code needs to be written by the user. Furthermore, the authors have made available Mathematica ® notebooks for download which perform the calculations.


Torsional Sader method

Recently [4], the Sader method has been extended to allow calibration of the torsional spring constant of rectangular AFM cantilevers, using the result

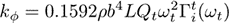
Torsional spring constant using the Torsional Sader method

where L and b are the length and width of the cantilever, respectively, ρ is the density of the fluid, ωt and Qt are the (radial) resonant frequency and quality factor of the fundamental torsional resonance peak, respectively, and Γit is the imaginary part of the hydrodynamic function given by Eq. (20) of Ref. [5].

Again, in order to assist the reader, the Torsional Sader method has been implemented in an online calibrator. Also, the authors have made available Mathematica ® notebooks for download which perform the calculations.


General Method for Arbitrary Small Bodies

The extension of the Sader method to cantilevers of arbitrary shape was recently presented [6], [7]. This includes an explanation of the underlying physical basis of the method, its validity in the presence of nonidealities, such as added spheres or tips, and its general applicability to small elastic bodies of arbitrary shape and composition.

iPhone and web apps that implement the general Sader method are available at the links above. The web app uses the Wolfram CDF Player plugin.



References
  1. J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 70, 3967 (1999)
  2. J. E. Sader, J. Appl. Phys., 84, 64 (1998) - See [3] for experimental validation of this theory.
  3. J. W. M. Chon, P. Mulvaney and J. E. Sader, J. Appl. Phys., 87, 3978 (2000)
  4. C. P. Green, H. Lioe, J. P. Cleveland, R. Proksch, P. Mulvaney and J. E. Sader, Rev. Sci. Instrum., 75, 1988 (2004)
  5. C. P. Green and J. E. Sader, J. Appl. Phys., 92, 262 (2002)
  6. J. E. Sader, J. Pacifico, C. P. Green and P. Mulvaney, J. Appl. Phys., 97, 124903 (2005)
  7. J. E. Sader, J. A. Sanelli, B. D. Adamson, J. P. Monty, X. Wei, S. A. Crawford, J. R. Friend, I. Marusic, P. Mulvaney and E. J. Bieske, Rev. Sci. Instrum., 83, 103705 (2012)

Home - Background theory - Online calibration - Mathematica files - Bibliography 


Created: 18 September 2003
Last modified: 8 March 2017
Authorised by: Head, School of Mathematics and Statistics.
Maintained by: John Sader, School of Mathematics and Statistics.
Email: jsader@unimelb.edu.au